

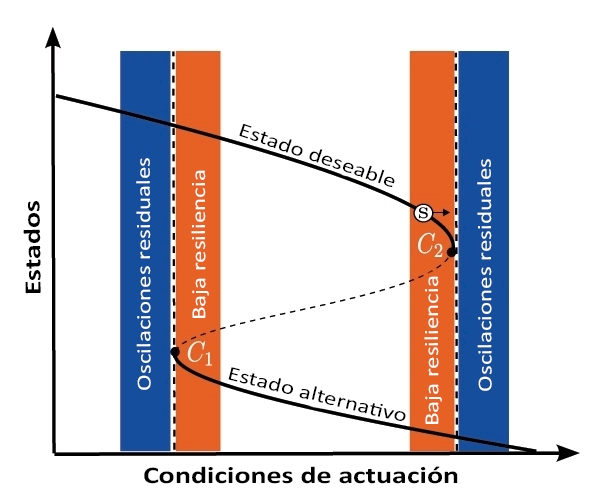
Representación de una transición crítica. Debido a factores adversos, el sistema S alcanza la condición de baja resiliencia (la franja anaranjada). En el punto crítico C2, el estado dinámico finalmente queda destruido y el sistema es atraído hacia un estado alternativo. Sin embargo, la dinámica deseable perdura en forma residual durante un cierto tiempo (la franja azul) y puede enmascarar el carácter irreversible de la transición
En una simulación, se demostró que la dinámica de un sistema perdura durante un determinado tiempo una vez sobrepasado el punto crítico. Y esta persistencia puede enmascarar el carácter irreversible de esa transición
En una simulación, se demostró que la dinámica de un sistema perdura durante un determinado tiempo una vez sobrepasado el punto crítico. Y esta persistencia puede enmascarar el carácter irreversible de esa transición
Representación de una transición crítica. Debido a factores adversos, el sistema S alcanza la condición de baja resiliencia (la franja anaranjada). En el punto crítico C2, el estado dinámico finalmente queda destruido y el sistema es atraído hacia un estado alternativo. Sin embargo, la dinámica deseable perdura en forma residual durante un cierto tiempo (la franja azul) y puede enmascarar el carácter irreversible de la transición
Por José Tadeu Arantes | Agência FAPESP – La expresión tipping point, o “punto de viraje”, se refiere a la transición crítica en la cual un sistema dinámico experimenta un cambio irreversible, a partir del cual se vuelve imposible volver al estatus anterior. Este concepto, sumamente amplio, puede referirse tanto a la extinción de una especie vegetal o animal, al agotamiento de un recurso hídrico o al colapso económico de una institución, entre muchos otros fenómenos naturales y sociales.
La simulación numérica de un tipping point, realizada por el investigador Everton Santos Medeiros, del Instituto de Física de la Universidad de São Paulo, en Brasil, permitió entender mejor las características de este punto sin retorno y qué sucede con el sistema luego de que éste se concreta. Este estudio fue comunicado en el artículo intitulado “Trapping Phenomenon Attenuates the Consequences of Tipping Points for Limit Cycles”, publicado en Scientific Reports, en febrero de 2017. Santos Medeiros cuenta con el apoyo de la FAPESP mediante una beca de posdoctorado.
“Los sistemas oceánicos, atmosféricos, ecológicos, económicos y otros pueden pasar por transiciones de esta índole. El sistema experimenta alteraciones graduales en sus parámetros hasta llegar a un límite en el cual un pequeño cambio provoca una transición abrupta e irreversible. El concepto de tipping point es conocido en la literatura. En nuestro estudio procuramos investigar qué sucede inmediatamente después de esta transición crítica”, declaró Santos Medeiros a Agência FAPESP.
Para modelar este tipo de transición, el investigador ideó un sistema dinámico cíclico genérico. La opción por el sistema cíclico obedeció al hecho de que gran parte de los fenómenos naturales exhiben un comportamiento recurrente, en función de encontrarse sometidos a forzamientos periódicos, tal como es el caso, por ejemplo, de la amplitud de la insolación, asociada a las estaciones del año.
“Por eso adoptamos un sistema dinámico cíclico genérico, pasible de describírselo mediante una ecuación diferencial simple. E hicimos una simulación numérica, variando uno de los parámetros de la ecuación, hasta llegar al punto en el cual el comportamiento que ésta describe se extinguía en el tipping point", describió Santos Medeiros.
Resulta importante considerar en este punto la salvedad que efectuó el profesor Iberê Luiz Caldas, supervisor del posdoctorado de Santos Medeiros y coautor del artículo: “Nuestro estudio no abordó sistemas dinámicos complejos, sino sistemas dinámicos simples que pueden exhibir comportamientos complejos. Esto es, sistemas dinámicos descritos por ecuaciones diferenciales no lineales que admiten soluciones complejas”, afirmó. Estos sistemas fueron bien estudiados por el gran físico, matemático y filósofo francés Henri Poincaré (1854-1912).
Una característica significativa de las transiciones clasificadas como tipping points es su naturaleza histerética. En otras palabras, una vez que se alcanza el límite crítico y el régimen dinámico se destruye abruptamente, su restauración ya no es posible mediante la mera reversión de la tendencia que causó el colapso. La extinción de una especie animal, el resecado de un espejo de agua o el deshielo de un gran glaciar siguen este tipo de patrón histerético: una vez que se alcanza el punto sin retorno, el daño se vuelve irreversible.
“Pero lo que nuestro estudio demostró, y éste es su aporte más importante, fue que, para ciertos fenómenos cíclicos, la dinámica del sistema perdura durante un determinado tiempo después de la transición crítica. Y esta persistencia puede enmascarar la propia transición. Consideremos una especie en extinción, por ejemplo. Dicha especie puede haber sobrepasado del punto sin retorno y estar irreversiblemente condenada. Sin embargo, sus ejemplares siguen existiendo y reproduciéndose en la naturaleza. Este efecto transiente esconde el hecho de que, a largo plazo, esa especie ya está extinta. En nuestro trabajo, mediante simulaciones numéricas, logramos observar ese efecto transiente posterior a la singularidad que configura el tipping point", explicó Santos Medeiros.
Dicho de otra manera: existe un punto de viraje a partir del cual los fundamentos del fenómeno experimentan un cambio irreversible; pero, debido a una especie de “efecto residual”, el proceso parece mantener sus características originales durante una etapa transitoria, enmascarando así la transformación ocurrida.
“El efecto transiente hace que el cambio histerético se confunda con el cambio gradual, pasible de una sencilla corrección. La transición puede parecer suave, pero, a decir verdad, puede ser crítica. En este caso, la eliminación de la causa no es suficiente como para revertir el colapso del sistema”, complementó Santos Medeiros.
“En las situaciones reales, resulta difícil saber si ya se ha alcanzado o no el punto sin retorno, el tipping point”, comentó el profesor Caldas. “El Bosque Atlántico, por ejemplo, en el tramo São Paulo-Santos, ¿puede recuperarse o está irremediablemente perdido? Como sigue existiendo mucha vegetación en esa zona, la impresión indica que puede recuperárselo mediante iniciativas capaces de remediar los daños ocurridos. ¿Pero eso será realmente posible? ¿Esa vegetación remanente no es tan sólo un efecto transitorio incapaz de revertir el colapso de la selva en el fragmento mencionado? La lección que aporta nuestro estudio indica que es necesario tener mucho cuidado cuando aparecen los síntomas de deterioro. Sucede que no todo deterioro puede revertirse algún día”, concluyó.
Republicar
The Agency FAPESP licenses news via Creative Commons (CC-BY-NC-ND) so that they can be republished free of charge and in a simple way by other digital or printed vehicles. Agência FAPESP must be credited as the source of the content being republished and the name of the reporter (if any) must be attributed. Using the HMTL button below allows compliance with these rules, detailed in Digital Republishing Policy FAPESP.





